問題
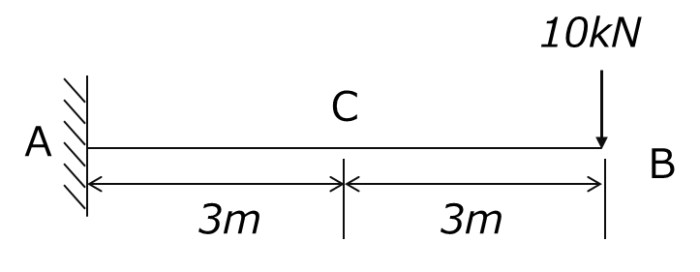
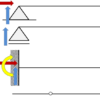
下図のように、点Bに10kNの集中荷重を受ける片持ちばりがある。このときの点Cにおける断面力を求めると共に、断面力図を作成せよ。
解説
構造力学の基礎的な問題の1つ。片持ちばりの問題です。
単純ばりのときと比べて、固定端の場合は発生する断面力にどのような違いがあるか理解しておきましょう。
順を追って解いていきます。
支点反力の算出
まず、支点反力を算出します。
今回のはりは固定端を持つ片持ち梁であるため、ピン支点やヒンジ支点とは違い、曲げモーメントも発生します。
これは、端部で鉛直、水平の動きに加えて、回転も固定しているということを意味しています。
支点の違いによる発生断面力への影響については、以下の記事を参考にしてください。
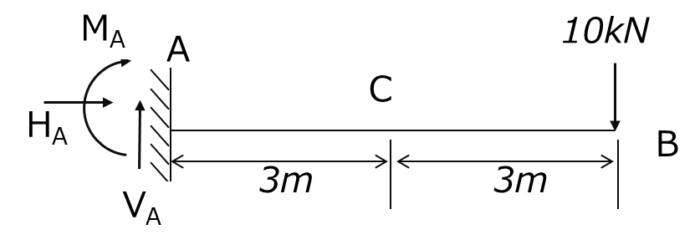
鉛直方向の力のつり合いより 10(kN)-VA=0 水平方向の力のつり合いより HA=0 点Bにおけるモーメントのつり合いより VA・6(m)+ MA= 0 ∴VA=10(kN), HA=0(kN), MA=-60(kN・m)
断面力の算出
次に、点Cにおける断面力を求めましょう。
※断面力図を作成するのに必ず必要なわけではないですが、断面力を算出する練習のために問題に入れています。
断面力の計算方法については、以下の記事に紹介しているので、参考にしてください。
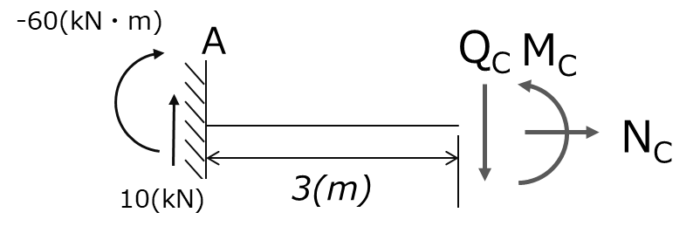
・軸力 NC 点Cにおける力のつり合いより NC=0 ・せん断力 QC 点Cにおける力のつり合いより QC – 10 = 0 ・曲げモーメント MC 点Cにおけるモーメントのつり合いより MC – 10 ×3 - (-60)=0 ∴NC=0(kN), QC=10(kN), MC=-30(kN・m)
断面力図の作図
算出した断面力を基に、断面力図を描いてみましょう。
断面力図の描き方については、以下の記事で詳しく解説しています。
今回は断面力を距離xで表すことはせず、なるべく楽に断面力図を描いていこうと思います。
せん断力図 Q-図
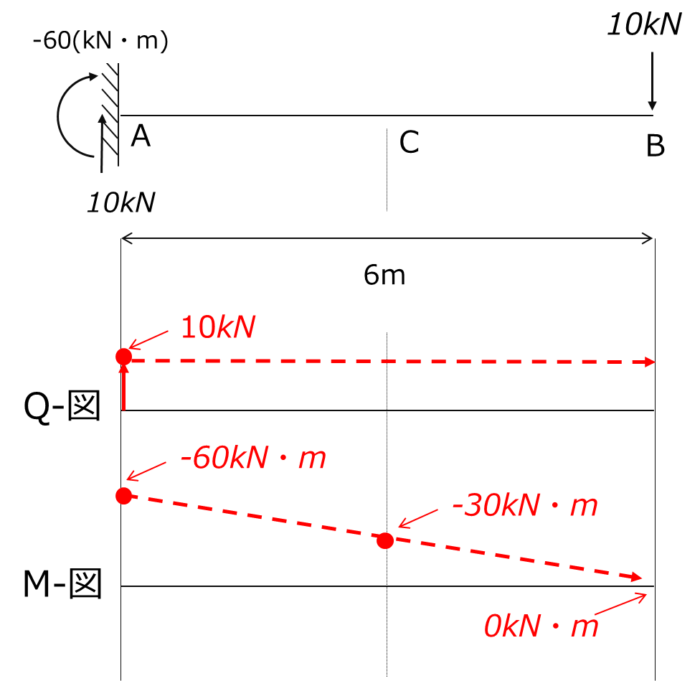
せん断力は、まず、点AでVAと同等の10kNとなりますね。
点Aからはりを右にずっと見ていくと、次に荷重があるのは点B:右端です。
ですので、せん断力は点Aから点Bまでずっと一定で、10kNとなります。
曲げモーメント図 M-図
次に、曲げモーメント図を描いていきます。
曲げモーメントは端部で支点反力と同じ値だけ発生します。そして、片持ち梁の自由端は鉛直方向も水平方向も回転も全く固定しません。
そのため、自由端では曲げモーメントは0kNと言うことになります。
まとめ
固定端では鉛直方向、水平方向、回転が固定されるため、鉛直反力、水平反力、曲げモーメントが固定端部で発生します。
一方、自由端ではこれらすべてが固定されていないので、反力は全てゼロになり、断面力も発生しません。
端部の条件によって断面力がどのように発生するか大きく変わってくるので、設計を行うときは端部の条件をどのように設定するかに注意しておきましょう。

-100x100.jpg)


