構造力学を学び始めてから早い段階で出会うのが、「断面力」という存在です。
この断面力、あまり構造力学になじみがなければイメージが難しいかもしれません。でもこの断面力、構造物の設計をする際にはわかっておかなければならない存在です。
今回は、この断面力とはそもそも何なのか、ということから、基礎的な知識や算出方法について解説していきたいと思います。
「断面力」とは？
下のような、部材の真ん中に集中荷重を受ける部材長 l の単純梁を考えてみます。
この単純梁、簡単のために線だけで描かれていますが、実際の構造物ではいろんな断面の形が考えられます。
図のように、線の途中でスパッと切ったときに見える面を断面と言います。図ではただの長方形の断面ですが、実際の構造物ではいろんな断面があります。
この断面に働く力が「断面力」です。
世の中の材料は分子と分子が引っ付いて、ひとつになってできています。断面力は、その材料が離れ離れにならないように働いてくれているんです。
また、部材の外から力が加わる「外力」に対して、断面力は部材の内部に働くので「内力」と言われています。
ではこの断面力、具体的にはどのような「力」なのか、説明していきましょう。
３つの断面力
断面力には３つの成分があります。（今回は平面上で考えるため、ねじりモーメントについては考えません。）
その3つの成分とは、下の3つです。
- 軸力（axial force）
- せん断力（shear force）
- 曲げモーメント（bending moment）
それぞれ、軸力＝N、せん断力＝Q、曲げモーメント＝Mと表され、下のような図で表現されます。
軸力 N
部材軸と同じ方向にかかる力で、向きによって軸圧縮力、軸引張力となります。構造物設計の際には、座屈に対する安全性を判断する際にこの軸力を取り扱います。
梁は曲げに抵抗する部材なので、基本的には軸力を問題にすることはありません。
ちなみに、構造力学では通常引張側を＋として扱う場合が多いです。コンクリート工学では反対で、圧縮側を+として扱うことが多いですね。
これは、構造力学では圧縮よりも引張に強い鋼材料を想定しているのに対し、コンクリートは圧縮に強く引張に弱いという特徴があるからなんです。
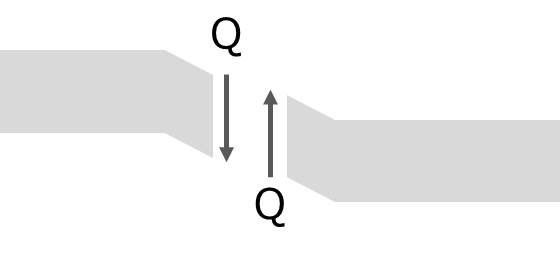
せん断力 Q
部材軸に垂直にかかる力で、部材がずれるような変形に抵抗します。軸力と比べてあまりイメージがつきにくいのですが、はさみで紙を切るときなどに紙にかかっているような力（変形）をイメージしてもらえるといいと思います。
せん断力は、断面が右下がりの変形をする方向を正とします。
構造物設計ではせん断力の正負が問題になることは少なく、その絶対値を相手にすることが多いのですが、正負の表現の仕方は右下がり変形を正というのが一般的なので、覚えていきましょう。
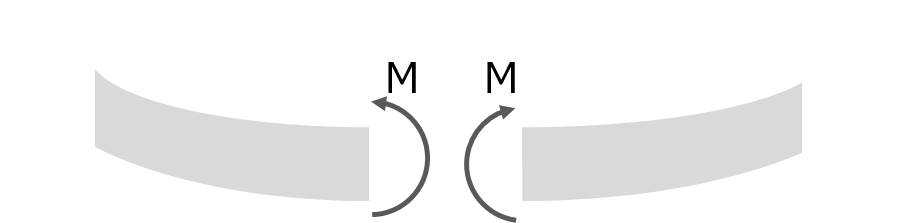
曲げモーメント M
部材が回転するような変形に抵抗するものです。断面力と言いながら、3つのうちこの曲げモーメントだけ力（force）ではありません。単位は[N・mm]などがよく用いられ、力×距離で算出されるものです。
曲げモーメントは、下の凸の方向に曲げるモーメントを正、反対を負とします。
余談ですが、曲げモーメントはせん断力を距離で積分したものとなります。
「モーメント」という言葉も概念がわかりにくいので、ピンとこない方は以下の記事を参考にしてください。
断面力の求め方
では、実際に断面力を求めてみます。
まず、VA、VB、HAについては、力のつり合いとモーメントのつり合いで簡単に求めてしまいましょう。
鉛直方向の力のつり合いより P-VA-VB=0 水平方向の力のつり合いより HA=0 点Bにおけるモーメントのつり合いより VA・l - 1/2P・l = 0 ∴VA=1/2P, VB=1/2P, HA=0
次に、断面力を求めてみたいと思います。ところが、断面力は部材を切る位置によって変わってきてしまいます。そこで、点Aからの任意の点までの距離をxとおいて、以下の図を用いて断面力を表現してみましょう。
・軸力 N 力のつり合いより N=0 ・せん断力 Q 力のつり合いより 0<x<1/2lのとき Q-1/2P=0 1/2l<x<lのとき Q+P-1/2P=0 ・曲げモーメント M モーメントのつり合いより 0<x<1/2lのとき M-1/2P・x=0 1/2l<x<lのとき M+P(x-1/2l)-1/2P・x=0 ∴0<x<1/2lのとき N=0, Q=1/2P, M=1/2Px 1/2l<x<lのとき N=0, Q=-1/2P, M=-1/2Px+1/2Pl
これで、断面力を点Aからの距離xを用いて表現できました！
これができれば、断面力の算出はばっちりです。
何に使うの？
断面力とはどういうものか、どのように算出するかを説明してきましたが、この断面力、何に使うのでしょうか？
実は構造物設計をする際は、この断面力を用いてやっていかなければなりません。
一般的に、構造物の設計をする際は、まず設計対象となる部材の全体をモデル化し、想定される荷重をかけたときの断面力を算出します。そして、断面力が一番大きいなど、部材内で条件が一番不利となる断面において、発生する断面力に耐えうる断面になるよう設計を行っていきます。
まとめ
以上が断面力についての基本的な解説です。
この断面力を用いて、断面力図を描いたり、応力照査をしたりと色々な面で活躍していきます。構造力学を学ぶ最初の段階でしっかり理解をしておきましょう！
続いて、部材全体の断面力をグラフで示してくれる断面力図の描き方について以下の記事で説明していきます。
コメント
断面力を考える時、なぜVbは考えないんでしょうか。
コメントありがとうございます。
断面力を解いている式の中で「Vb」が出てこないのは、
Va側での力のつり合いで考えているからです。
このような構造力学の問題は「静力学」ですので、力がつり合っている状態です。
これは任意の点で切って考えてやっても同じことが言えます。
記事内の解き方で見ているのは、問題となっている単純梁を切った「左側」です。
この「左側」で力がつり合っている状態を方程式を置くことで考えています。
仮にこれを「右側」の力がつり合っている方程式を立てて（すなわち、Vbが出てくる式で）解いても同じ答えになるでしょう。
説明がわかりにくかったら、同じことをVb側でもやってみてください。
なお、ご質問の意図が「Va側とVb側両方から解いた方が簡単では？」という趣旨でしたら、
この例では説明のために計算は複雑になるけど考え方は単純なやり方として左側からのみ解いていった、とお考え下さい。
もっと効率のいい解き方もありますからね。
何かご不明点あれば再度ご連絡下さい！