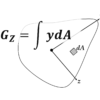【構造力学】図形の図心軸回りの断面２次モーメントを求める

問題

下図の図心軸z₀z₀回りの断面2次モーメントを求めよ。

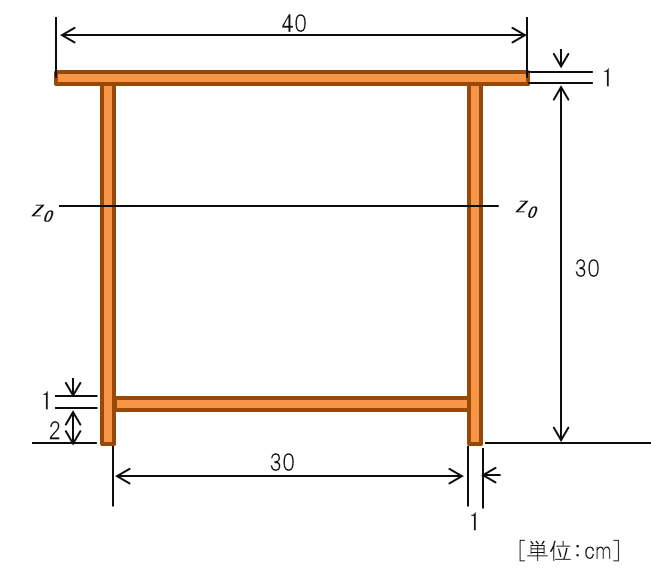
解説

断面2次モーメントを算出する基本的な問題です。

断面2次モーメントは、曲げに対する部材断面の抵抗を示す重要な断面量です。

単純な矩形や円形などは公式を調べると簡単に出てくるので苦労しないと思いますが、公式だけでは図心がわからない図形や任意の図形に対応できません。

しっかりと手計算でも断面2次モーメントの算出ができるようにしておくのが望ましいですね。

断面2次モーメントは以下の式で定義されています。

I_z= ∫y²dA

積分が出てくるので拒否反応がある方もいるかもしれませんが、もう少し我慢してください。

図心軸をz₀軸として図心軸回りの断面2次モーメントをI_z0とします。また、z₀軸に平行でz₀軸からy₀離れた軸をz軸とし、そのz軸回りの断面2次モーメントをI_zとします。

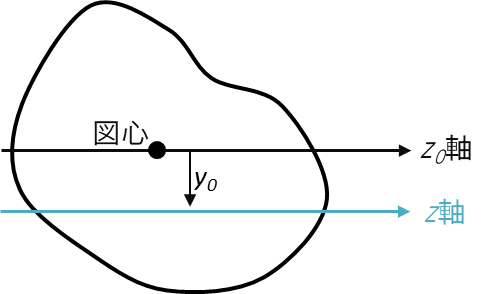
すると、これらには以下のような関係があります。

I_z= I_z0+ y₀²A

この式を用いて、問題の図形の断面２次モーメントを計算していきましょう。

断面２次モーメントを以下の流れで算出していきます。

任意の軸を設定し、その任意軸回りの断面２次モーメントを求める
図形の図心を求める
１，２の結果から、図心軸回りの断面２次モーメントを求める

それでは、問題の解答をしていきます。

解答

断面２次モーメントを求めるには、色々な方法があります。言い換えると、どのように計算しても、計算の複雑さの差はありますが、算出することは可能です。

今回は軸の設定を変えた２種類の方法で解いていきましょう。

解答１

1. 任意の軸を設定し、その任意軸回りの断面２次モーメントを求める

まず、任意のz軸を設定します。解答１では、30mm×1mmの縦長の部材の中心にz軸を設定してみましょう。

長方形の図心軸回りの断面２次モーメントはbh³/12で簡単に求められるので、下図のように３つの長方形に分類し、z軸から各図形の図心までの距離y、面積A、各図形の図心軸回りの断面２次モーメントI₀、z軸回りの断面２次モーメントを求めるためにy²Aを求めます。

それぞれ計算しますが、下の表のように表すと簡単にまとめられます。表では、図の下向きを正としています。

この表から、任意軸として設定したz軸回りの断面２次モーメントI_zを算出します。

I_z= I₀+ y²A
=4505.83 + 14297.5
=18803.333 [cm⁴]

２. 図形の図心を求める

次に、図形の図心を求めていきます。

図形の図心を算出するには、断面１次モーメントを用います。

図心軸のz軸からの距離をy₀とし、z軸に対する断面１次モーメントをG_zとすると、以下の式からy₀の位置が算出できます。

y₀= G_z / A
= ∑Ay / ∑A
=-245 / 130
=-1.88461 [cm]

すなわち、z軸からマイナス向き（上向き）に1.88cmいったところに図心軸z₀があることがわかりました。

３.１，２の結果から、図心軸回りの断面２次モーメントを求める

ここまで来ると後は簡単です。

1.で使った I_z= I₀+ y²Aを思い出しましょう。

これを図心軸回りの断面２次モーメントI_z0に適用すると、以下の式から図心軸回りの断面２次モーメントを算出できます。

I_z0 = I_z – y₀²A
=18803.33 – 1.88461²×130
=18341.6　 [ cm⁴]

ということで、正解は18341.6 [ cm⁴]となります。

※四捨五入のやり方で答えが少し異なることがありますが、ここでは厳密に定義していません。

解答２

解答２では最初に設定するz軸を解答１と異なるところに設定して計算していきます。

計算の内容は省略しながら書いていきます。流れは解答１と全く同じです。

1. 任意の軸を設定し、その任意軸回りの断面２次モーメントを求める

任意のz軸を、1mm×40mmの横長の部材の中心に設定します。

解答１の計算の過程で気付いた方も多いと思いますが、分割したそれぞれの図形（この問題で言う①②③）の図心を通る軸を設定すると、後々計算が楽になります。

先程と同じように、表にまとめてみましょう。ここでも、下向きを正としています。

この表を基に、z軸回りの断面２次モーメントを求めます。

I_z= I₀+ y²A
=4505.83 + 37935
=42440.833 [cm⁴]

z軸回りの断面２次モーメントは42440.8 [cm⁴]となり、同じ図形であるにもかかわらず解答１（18803.33）とは違う値になりました。
これは、解答１と解答２でz軸の設定が異なることが理由です。

２. 図形の図心を求める

さっきと同じように、図心軸とz軸との距離y₀を算出していきます。

y₀= G_z / A
=∑Ay / ∑A
=1770 / 43.5
=13.615 [cm]

z軸から13.6cm下に行ったところに図心軸があることがわかりました。

３.１，２の結果から、図心軸回りの断面２次モーメントを求める

これも同様に計算していきましょう。

I_z0= I_z– y₀²A
=42440.833 – 13.615²×130
=18341.6　 [ cm⁴]

ということになり、解答１と同じ結論が得られます。

最初のz軸の取り方に関わらず、同じ答えが導き出せることがわかりました。

まとめ

図心軸回りの断面２次モーメントを、２種類の任意軸の設定で解いてみました。

この問題は上述のように、まず、図形を簡単な図形（長方形、円等）に分割し、面積A、軸からの距離y、y²A、I₀を表にまとめた上で、以下の順番で解いていくとスムーズです。
1. 任意の軸を設定し、その任意軸回りの断面２次モーメントを求める
２. 図形の図心を求める
３.１，２の結果から、図心軸回りの断面２次モーメントを求める

公式だけを覚えていると途中で何を求めているかわからなくなります。理由や仕組みをしっかり理解しておきましょう。