【構造力学】断面力図の問題その１－分布荷重

問題

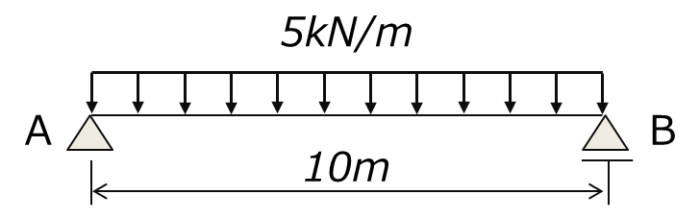
下図のように、単純ばりに5kN/mの分布荷重が一様に作用している。この時の断面力図を作成せよ。

解説

構造力学の基礎的な問題の1つ。分布荷重をどのように扱うかがキーとなります。

分布荷重を扱うときには、「合力」の考え方を用いると簡単に解くことができます。

それでは、順を追って解いていきましょう。

支点反力の算出

まず、支点反力を算出します。

モーメントのつり合いを考える際、下図のように分布荷重の合力を考え、集中荷重に置き換えて考えていることに注意しましょう。

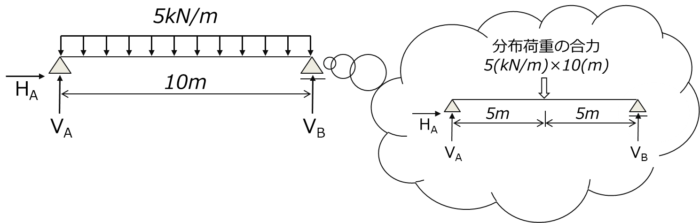
鉛直方向の力のつり合いより
 5(kN/m)×10(m)-VA-VB=0 
水平方向の力のつり合いより
 HA=0
点Bにおけるモーメントのつり合いより   
 VA・10 (m)- 5(kN/m)×10(m)×10(m)/2= 0
 
  ∴VA=25(kN), VB=25(kN), HA=0 

ただ、このくらい単純な問題の場合は、
「左右対称だからV_A=V_Bのはず。鉛直方向の力のつり合いを考えて、V_A=V_B=25kN」
として考えても問題ありません。

断面力の算出

次に、断面力を求めていきます。

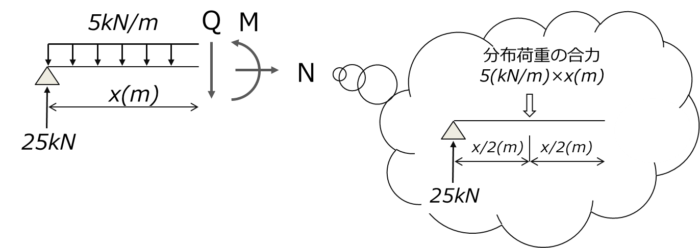
断面力の計算方法については、以下の記事に紹介しているので、参考にしてください。

・軸力　N 　　
 力のつり合いより  N=0 
・せん断力　Q 　
 力のつり合いより 　　
    Q + 5x - 25 = 0 
・曲げモーメント　M 　
 B周りのモーメントのつり合いより
  　M + 5x × x/2 - 25x=0
 
 ∴N=0, Q= -5x+25(kN), M= -5x2/2+25x

断面力図の作図

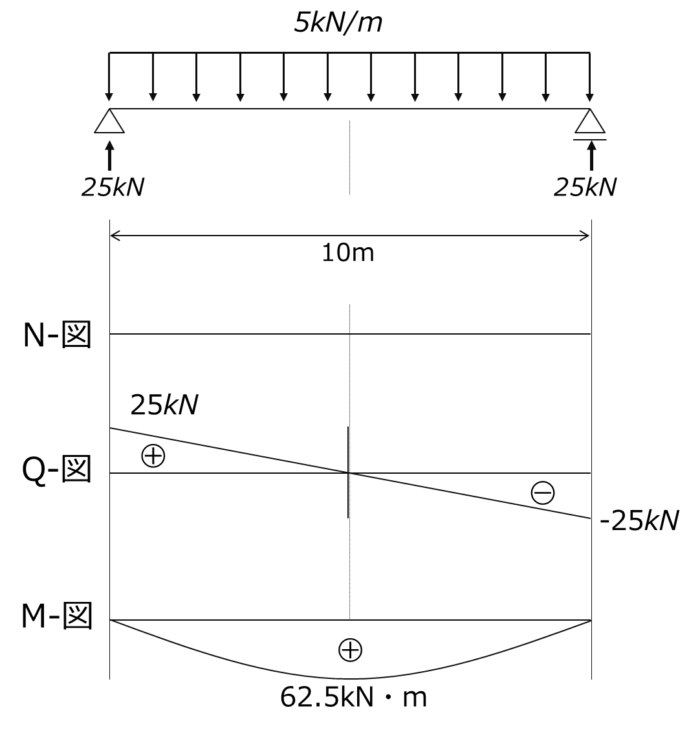
算出した断面力を基に、断面力図を描いてみましょう。

断面力図の描き方については、以下の記事で詳しく解説しています。

断面力図の作図その②

断面力図を描く方法として基本的な考え方は以上のような手順でしょう。

ただ、わざわざ断面力xで表現するような手間をかけなくても、基礎を理解してさえいれば断面力図は簡単に描くことができます。

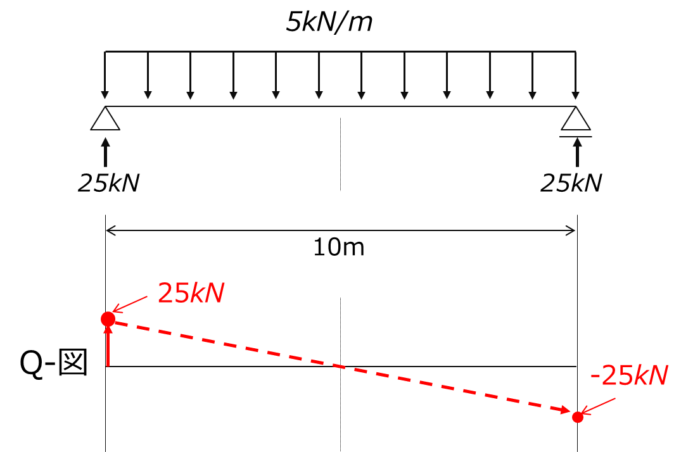
せん断力図　Q-図

せん断力図は、分布荷重の場合は直線的に変化をします。

この問題では分布荷重は一様な等分布荷重なので、Q-図は点Aから点Bまで傾き一定の直線になることがわかりますね。

このことさえ理解していれば、点AでQ＝25kN、点BでQ=-25kNというのは正負さえ間違えなければ簡単に計算できるので、下図のような形になります。

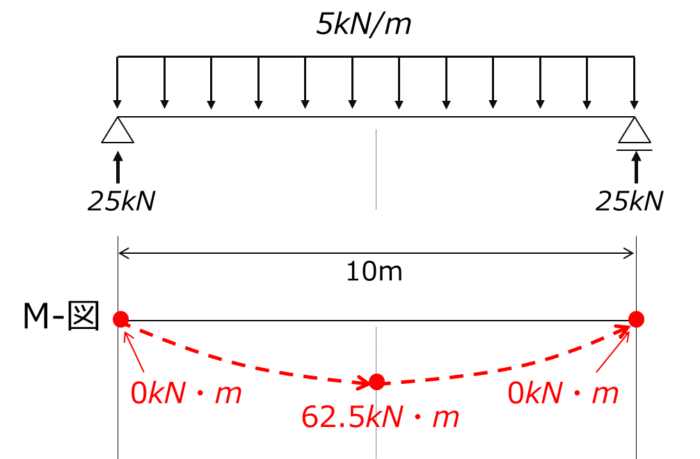
曲げモーメント図　M-図

曲げモーメント図については、等分布荷重の場合、曲線となります。

今回は等分布荷重なので、左右対称となることも予想できますし、一番大きな曲げモーメントが発生するのは中点だということは「想像」できると思います。

想像できない人は、薄い鉄板の両端だけを支えて持っていることを想像してみてください。鉄板は自重（＝等分布荷重）によって中点が下がるように変形しますね。これが曲げモーメント図の形です。

モーメントのつり合いを使って、両端と中点だけモーメントを算出し、それを曲線（2次曲線）で結べば完成です。

まとめ

分布荷重が出てきたときは「合力」の考え方を使って解くとわかりやすく解くことができます。

設計の実務では設計上考慮する荷重を分布荷重として計算する場合も多いので、その時の断面力図の形をイメージできるようにしておくことは、設計者として重要な能力でしょう。

類似問題