断面1次モーメントと呼ばれる断面量を聞いたことがあるでしょうか?
構造力学を学んだ人の中には、学習し始めた最初の方にさっと出てきて、その後はあんまりお世話になってない断面量である人も多いと思います。
今まさに構造力学を学んでいる人の中には、断面1次モーメントが何を示す値なのかイメージがつかない人も多いのではないでしょうか?
本記事では、そんな断面1次モーメントの定義や意味、使い方について解説していきたいと思います。
導出方法については詳しく解説していませんので、ご注意ください。
定義
まず、断面1次モーメントの定義です。定義式は以下のようになります。
Gz = ∫ydA
ここで、Gz:z軸に対する断面1次モーメント、y:軸からの距離、dA:微小面積
つまり、図形の「距離」×「面積」を足し合わせたものと言う定義になります。
距離というのはz軸からの距離を表しており、z軸が図心を通る軸の場合は断面1次モーメントは0になるという特徴があります。この特徴を活かして、図心の位置を算出することもできます。
使いどころ
では、この断面1次モーメントはどのように使っていくことができるのでしょうか?
主に用いられるのは、図形の図心を求めるときです。
断面を構成する材料が一定であれば、図心はその断面の重心と同じになります。重心は、断面内でどのように応力が発生しているかを把握するために非常に重要な意味を持ちます。
どのように図形の図心を求めることができるのか考えていきましょう。
まず、定義から、図形の面積Aとその図形の図心とz軸との距離y0を用いると、以下のようなことが言えます。
Gz = Ay0
y0 =Gz / A
この2式は順番を入れ替えただけです。
ここで、「図心に対する断面1次モーメントは0では?」と思ってしまう人がいます。
ここで出てくる断面1次モーメントGz は、図心軸に対するものではなく(別の)z軸に対するものなので、0にはなりません。
この式の導出過程で「図心軸に対する断面1次モーメントは0」という特徴を使っているので、気になる人は調べてみてください。
上で計算した式のように、自分で設定したz軸に対する断面1次モーメントを求め、総面積で割ることにより、図心の位置y0を算出することができます。
断面1次モーメントの意味
恐らく断面1次モーメントの定義や用い方を覚えて利用するのは簡単だと思いますし、構造力学の参考書を見ればいくらでも書いてあります。
ただ、この断面量の意味を示している参考書や書き物は少ないのではないでしょうか?
ここではその意味をイメージしてもらうための考え方を説明していきます。
シーソーを考える
まず、以下のような棒と支点の両端に、W1とW2というおもりが載せられていることを想像しましょう。シーソーのような状態です。
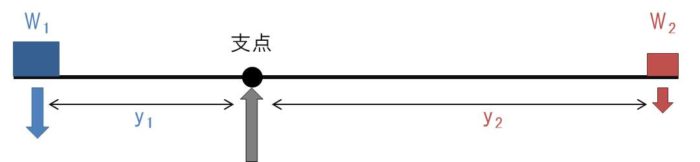
この棒の重さを簡単のために0と考えると、それぞれのおもりに起因する回転モーメントは、「距離」×「重さ」でy1W1 と y2W2 となります。
すなわち、支点回りに発生する回転モーメントは y1W1 +y2W2 と表すことができますね(yの符号は逆)。
同じように、今度はおもりの数を、W11 、W12、…、W1n、W21、W22、…、W2nのように増やしてみます。
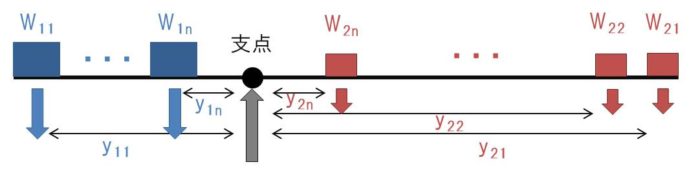
支点回りに発生する回転モーメントは W11 +W12+…+W1n+W21+W22+…+W2n=∑yWで表現することができます。
この棒が回転せずに静止するためには、支点回りの回転モーメントが0になる必要があります。つまり∑yW=0となるはずです。
断面1次モーメントに当てはめる
さて、ここまでの話がどのように断面1次モーメントに結びつくのでしょうか?
これまで説明してきたシーソーの話で、以下の図のように「回転モーメント」⇒「断面1次モーメント」、「重さ」⇒「面積」、「棒」⇒「面」として考えてみてください。

断面1次モーメントは「距離」×「面積」で表現できていることと、回転モーメントが「距離」×「重さ」で表現できることが全く同じことと考えられませんか?
回転モーメントがy×Wの合計で表現できるように、断面1次モーメントはy×Aの合計で表現できます。
また、シーソーが止まるためには支点(重心)回りの回転モーメント∑yW=0になるように、図形の図心に対する断面1次モーメントGz=0となります。
つまり、断面1次モーメントは図形が面積に応じた重さを持つと考えたときの回転モーメントと同じ意味を持つと考えられます。
まとめ
断面1次モーメントについて、定義や意味を説明してきました。
- 断面1次モーメントは「距離」×「面積」で表される
- 図心軸に対する断面1次モーメントは0となる
- 断面1次モーメントは、図形が面積に応じた重さを持つと考えたときの回転モーメントととらえると理解しやすい
たかが断面1次モーメントですが、意味を知っていると応用が利きますし、構造力学の更に難しい範囲の理解も容易になります。しっかりと理解しておきましょう。


