問題
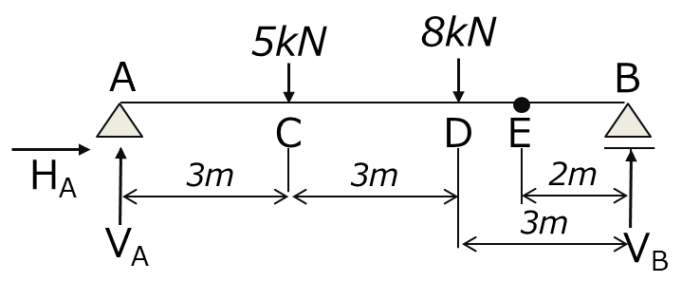
下図のように、点Cと点Dにそれぞれ5kNと8kNの集中荷重を受ける単純ばりがある。このときの点Eにおける断面力を求めると共に、断面力図を作成せよ。
解説
構造力学の基礎的な問題の1つ。単純ばりに対して複数の集中荷重が作用している場合の問題です。
基本的には集中荷重が1つの場合と何ら変わりありませんが、計算の仕方でちょっとした工夫ができます。
手計算する際に簡単に計算するテクニックと、その裏にある断面力の対称性について、この問題で学んでほしいと思います。
順を追って解いていきます。
支点反力の算出
まず、支点反力を算出します。
単純ばりですし、集中荷重は2つありますが、力のつり合いとモーメントのつり合いから簡単に求められます。
鉛直方向の力のつり合いより 5(kN)+8(kN)-VA-VB=0 水平方向の力のつり合いより HA=0 点Bにおけるモーメントのつり合いより VA・9 (m) – 5(kN)×6(m) – 8(kN)×3(m) = 0 ∴VA=6(kN), HA=0(kN), VB=7(kN)
断面力の算出
次に、点Eにおける断面力を求めましょう。
今回は2パターン、点Eの左側のつり合いから断面力を求めるパターンと、右側のつり合いから断面力を求めるパターンで解いていきます。
点Eの左側
まず、点Eの左側のつり合いから断面力を計算していきます。
これさえ覚えておけば静定ばりの断面力はたいてい算出できるでしょう。
集中荷重が1つだけの場合より、荷重が増えた分ちょっとだけ計算が複雑になります。
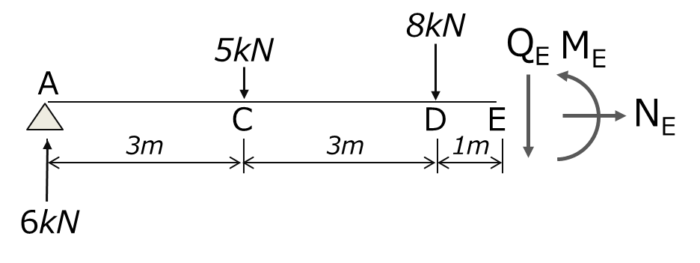
・軸力 NE 点Eにおける力のつり合いより NE=0 ・せん断力 QE 点Eにおける力のつり合いより QE – 6(kN) +5(kN) +8(kN) = 0 ・曲げモーメント ME 点Eにおけるモーメントのつり合いより ME – 6(kN)×7(m) + 5(kN)×4(m) + 8(kN)×1(m) = 0 ∴NE=0(kN), QE=-7(kN), ME=14 (kN・m)
点Eの右側
今度は点Eの右側のつり合いから断面力を求めていきます。
ここで1つ注意点。
左側で解く場合と右側で解く場合では、断面力の向きが異なります。
これは、点Eにおける断面力がつり合っていることが理由です。
点Eは静止しているので、内力である軸力、せん断力、曲げモーメントはつり合っています。青の点線の中の断面力がつり合うように断面力の向きが決まっているのです。
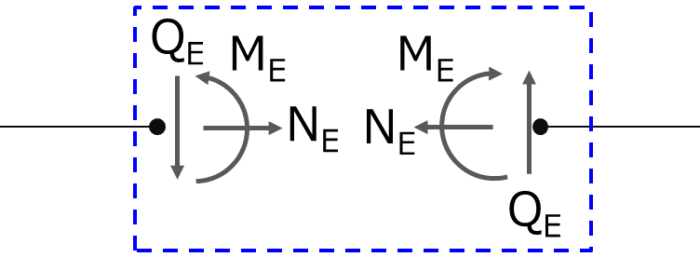
この向きを忘れずに、点Eの右側でつり合い式を解いてみると、さっきよりも簡単に算出できることがわかります。
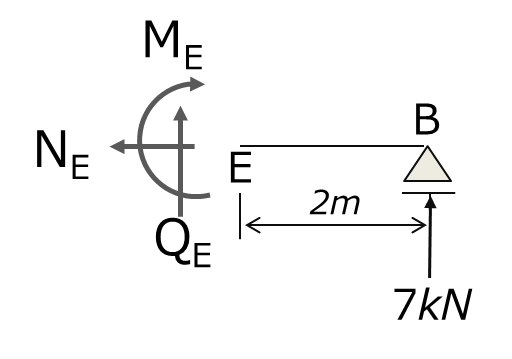
・軸力 NE 点Eにおける力のつり合いより NE=0 ・せん断力 QE 点Eにおける力のつり合いより QE + 7(kN) = 0 ・曲げモーメント ME 点Eにおけるモーメントのつり合いより ME – 7(kN)×2(m) = 0 ∴NE=0(kN), QE=-7(kN), ME=14 (kN・m)
断面力図の作図
それでは、断面力図を描いてみましょう。
断面力を距離xで表してグラフ化してもいいのですが、そうすると点A~点C、点C~点D、点D~点Bと場合分けが必要となるため、簡単な解き方とは言えません。
今回は極力そういった場合分けや計算をせず、なるべく楽に断面力図を描いていこうと思います。
せん断力図 Q-図
この単純ばりに作用しているのは支点反力と集中荷重のみなので、荷重が作用する点A~C間、点C~D間、点D~B間ははりと平行な直線となるはずです。
また、支点反力や集中荷重が作用する点で、作用している荷重の向きに、荷重と同じ大きさだけ移動します。
以上のことを踏まえ、せん断力図は、具体的に以下のような手順で描いていきます。
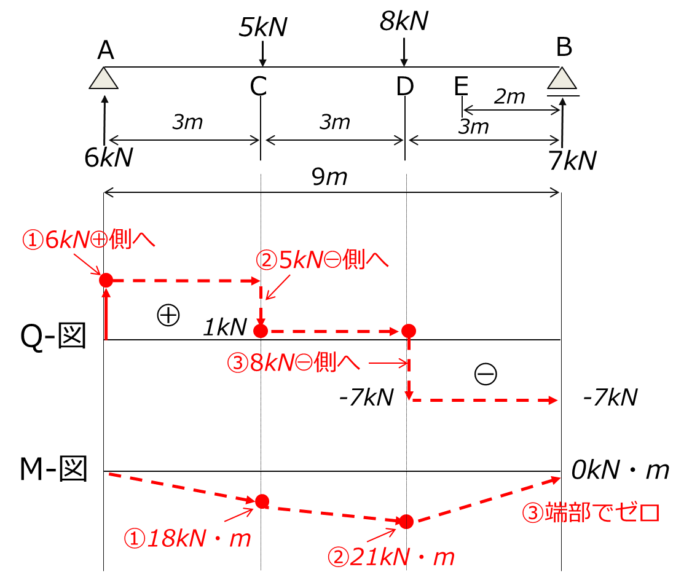
①まず、点AでVAと同等の6kN
②点Cで集中荷重と同じ5kNマイナス側に移動
③点Dで集中荷重と同じ8kNマイナス側に移動
④点BではVbと同等で向きが逆の-7kN
曲げモーメント図 M-図
次に、曲げモーメント図を描いていきます。
曲げモーメント図は、集中荷重が作用する場合、点A~C間、点C~D間、点D~B間で一定の傾きを持った直線となります。
また、単純ばりのピン支点、ローラー支点では回転は拘束されないので、端部の点A、点Bでは曲げモーメントは0になることもポイントです。
以上のことを踏まえ、点C、点Dにおける曲げモーメントを算出することにより図を作成していきます。具体的には以下のような手順になります。
①点Cで、モーメントのつり合い(点A側)より、MC=6×3=18kN・m
②点Dで、モーメントのつり合い(点B側)より、MD=3×7=21kN・m
③点Bはローラー支点なので、MB=0kN・m
以上のような手順で作成した断面力図(Q-図とM-図)は以下のようになります。
まとめ
集中荷重が複数になると、その分計算が少し複雑になります。
今回のように集中荷重が2つだけだとまだ簡単ですが、3つや4つの集中荷重や分布荷重が一緒になると、手計算ではかなりややこしくなるでしょう。
そんな時は、構造力学的な意味をしっかりと理解した上で、簡単に計算できる方法を探せると非常に便利です。
この問題に関連する断面力図の作成方法については、以下の記事にまとめているので、内容がわからなかったという方は参考にしてください。




