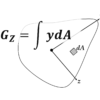土木工学分野の中で、よく聞く言葉の一つに「モーメント」というものがあります。力のモーメント、曲げモーメント、断面2次モーメント・・・などいろいろなところに出てくる「モーメント」ですが、力でもなければエネルギーでもない、なんとも理解しづらいものでもあります。
でも「モーメント」を使うのはもはや常識となってしまい、今更深く考えることもなく、概念は理解せずとも実務や問題の解答で使っている人は多いのではないでしょうか?
今回は、このモーメントとは何なのか、概念について書くとともに、「モーメント」の言葉がつく物理量について何を示しているのかを、なるべく数式を使わずにまとめました。
モーメントとは何か?
辞書で調べてみました。
まず、辞書に載っている基本的な意味を調べてみました。
- 非常に短い時間。瞬間。瞬時。
- 契機。きっかけ。
- ある点を中心として運動を起こす能力の大きさを表す物理量。定点から任意の点までの位置ベクトルと、その点におけるベクトル量との積で表される。力のモーメント、磁気モーメントなど。能率。
- ツイッターで、特定の話題に関するツイートをまとめる機能。
goo辞書より
・・・なるほど。
我々が対象としているのは、明らかに3番目ですね。これだけではなんのことかさっぱりわかりません。
何を示しているのか説明していきましょう。
モーメントの意味
モーメントという言葉の意味、概念はどのように理解しておけばいいのでしょうか?
モーメント全体の説明をする前に、まず、力のモーメントを例にとってみましょう。
力のモーメントとは、「力×距離」で表される物理量(ベクトル量)で、物体の回転運動を生じさせるものです。
なかなか概念がわかりにくいのは、力や仕事、エネルギーとはまた違う物理量だからかもしれません。
そんな力のモーメントを言葉で定義すると、「物体を回転させようとする力の働き」となります。(力のモーメントについての詳細は後述します。)
ここで、「力の」を抜いた「モーメント」に一般化して考えてみると、モーメントとは、様々な対象に影響する「働き」や「能力」、「効果」などといった言葉で言い換えることができます。
日本語で「能率」と訳されている場合も多くありますね。
○○モーメントの意味
それでは実際に、○○モーメントと名前の付いた言葉の意味を説明していきます。ここでは意味に着目しているので、値の求め方や計算方法は省略しています。
力のモーメント
モーメントと言われて多くの方が最初に思いつくのはこれではないでしょうか?
前述の通り、力のモーメントとは、「物体を回転させようとする力の働き」として定義されています。
力のモーメントの存在を説明するのに必要なのは、物体の2種類の運動、「並進運動」と「回転運動」です。少し正確性を欠きますが、極簡単に言うと、並進運動は物体そのものが真っすぐ動く運動、回転運動は物体が回転する運動を指します。
この2つの運動、当然運動が始まる原因となるのは力の作用です。
ですが、「並進運動」と「回転運動」では、この力の物体の運動への働き方が異なります。
「並進運動」では力が作用した向きに物体のすべての点が同じ運動をしますよね。
一方、「回転運動」は同じ物体の異なる点では異なる運動をします。すなわち、作用する力の大きさや向きだけではなく、作用位置も物体の運動に影響してくるのです。
このような「回転運動」における物体の異なる点における運動は、「距離×力」の力のモーメントを用いることで説明することができます。
言い換えると、「並進運動」では、力の働きが力そのものによってもたらされるのに対して、「回転運動」では力そのものでなく、力のモーメントとして物体にもたらされているのです。
曲げモーメント
よく力のモーメントと間違えられる曲げモーメントですが、両者は全く異なる物理量です。
何が違うかというと、力のモーメントは外力で、曲げモーメントは内力なんです。
力のモーメントは、物体に作用する外力による物体の運動、変形等を対象としているのに対して、曲げモーメントは外力を受ける物体の内部に発生している内力を対象として算出される値です。
曲げモーメントについてはこちらの記事で解説していますので、ご覧ください。
「モーメント」という言葉からのつながりから考えると、「物体を曲げ、変形させようとする内力の働き」と定義できますね。
断面二次モーメント
これも構造力学、材料力学などでよく使いますね。Iという記号で表されるのが一般的です。
断面二次モーメントとは、「変形のしにくさ」を表す物理量で、単位は[mm4]などが用いられます。断面二次モーメントが大きければ大きいほど変形はしにくく、小さければ変形しやすい断面形状であるということができます。
ヤング率Eと掛け合わせた剛性=EIはあらゆるところで用いられますので、非常に大切な物理量ですね。
言葉の定義としては、「曲げモーメントに対して抵抗する働き」とでも言えるでしょう。
断面一次モーメント
断面”二次”モーメントがあれば、断面”一次”モーメントもあります。
力のモーメントが「距離×力」で表されたのに対して、断面一次モーメントは「距離×(微小)面積」で算出されます。
意味が特に捉えにくい断面量の1つですが、こちらの記事で詳しく解説しました。気になる方はご覧ください。
部材の図心を求めるときに用いられますね。
慣性モーメント
慣性モーメントは、物体の回転運動を語る際に用いられる言葉です。
ニュートンの第一法則「静止しているものは静止し続け、運動しているものは運動し続ける」という慣性に関係しています。
等速直線運動をしている物体が、何も力を加えなければ等速直線運動を続けるように、回転運動をしている物体も、何もモーメントを加えなければ一定の角速度を維持しながら回転します。
等速直線運動でいう「慣性」が、回転運動で言う「慣性モーメント」であると考えておきましょう。
回転を維持しようとする(もしくは回転に抵抗する)働きであるということができそうです。
トルクとの違い
モーメントと言うと、トルクと混同してしまうことが多いかもしれません。
これはモーメント=トルクと言うのは、半分正解・半分不正解と言ったところでしょうか?
というのも、トルクと言うのは力のモーメントの一種で、回転軸周りのねじりの強さのことを言います。
ねじりモーメント=トルクだと思っておくと間違いないでしょう。
まとめ
モーメントの意味や、モーメントという言葉の付く物理量について解説しました。
モーメントとは、力でもエネルギーでもない物理量であるわけですが、これを定義することによって構造力学や材料力学など様々な分野で役立てられています。
わかりにくい上によく使うので、何者なのかわからずに使われていることもありますが、こういった言葉が何を示しているのかをしっかり理解しておくことは大切ですので、もやもやした部分を残さないようにしておきましょう。
※数式をなるべく使わずに解説をしていますので、不正確な部分もあったかもしれませんが、概念としての理解にお役に立てていただきたいと思っています。
他にも、「モーメント」の付く言葉でわかりにくいものがあったらコメントなどでご連絡ください!

-100x100.jpg)